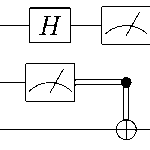
bell state quantum circuit: testing qiskit
Prerequisites and Environment
This guide assumes you have already set up your Python development environment with Qiskit installed. If you haven’t completed the initial setup, please refer to our Python Environment Setup for Quantum Computing guide first.
In this tutorial, we’ll test your Qiskit installation by creating and running your first quantum circuit. You’ll learn the fundamentals of quantum mechanics and witness quantum entanglement in action through a Bell state experiment.
Understanding Quantum Mechanics Basics
What is a Qubit?
A classical bit exists in either state 0 or 1. A quantum bit (qubit) can exist in a superposition of both states simultaneously. This fundamental difference enables quantum computers to explore multiple solution paths in parallel.
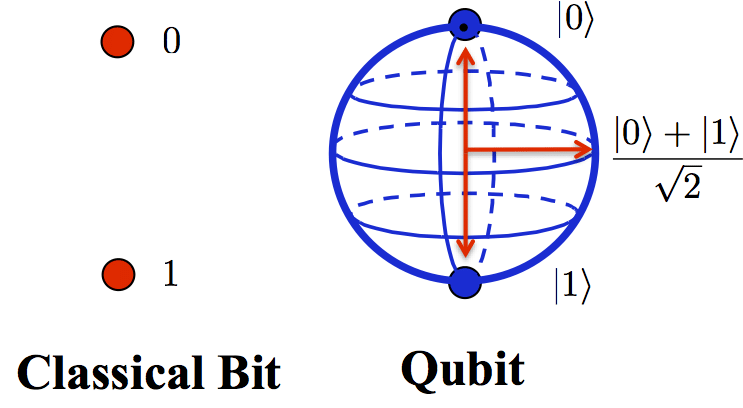
Mathematically, a qubit state is represented as:
$$|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$$
Where α and β are complex probability amplitudes, and |α|² + |β|² = 1
Quantum Entanglement
“Spooky action at a distance” – Albert Einstein’s description of quantum entanglement, the phenomenon where measuring one particle instantly affects another, regardless of distance.
Quantum entanglement occurs when qubits become correlated in such a way that the quantum state of each qubit cannot be described independently. The Bell state represents the simplest example of maximum entanglement between two qubits.
Creating Your First Quantum Circuit: Bell State
Theory: The Bell State Equation
The Bell state we’ll create is mathematically represented as:
$$ |\Phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) $$
This equation tells us that when measured, we’ll observe either both qubits in state 0 or both in state 1, each with 50% probability. We’ll never see mixed states like 01 or 10.
Implementation
# Import required libraries
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
# Create a quantum circuit with 2 qubits and 2 classical bits
qc = QuantumCircuit(2, 2)
# Step 1: Create superposition on first qubit
# Hadamard gate transforms |0⟩ → (|0⟩ + |1⟩)/√2
qc.h(0)
# Step 2: Create entanglement between qubits
# CNOT gate: if qubit 0 is |1⟩, flip qubit 1
qc.cx(0, 1)
# Step 3: Measure both qubits
# This collapses the quantum state to classical bits
qc.measure_all()
# Display the circuit
print("Bell State Circuit:")
print(qc.draw())
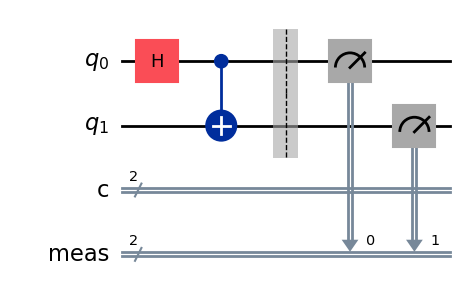
Circuit Visualization
┌───┐ ░ ┌─┐
q_0: ┤ H ├──■───░─┤M├───
└───┘┌─┴─┐ ░ └╥┘┌─┐
q_1: ─────┤ X ├─░──╫─┤M├
└───┘ ░ ║ └╥┘
c: 2/══════════════╬══╬═
║ ║
meas: 2/══════════════╩══╩═
0 1
- H: Hadamard gate creates superposition
- ■: Control qubit for CNOT operation
- ⊕: Target qubit (X gate when control is |1⟩)
- M: Measurement operation
- ░: Barrier (separates quantum and classical operations)
Running the Quantum Simulation
# Initialize the quantum simulator
simulator = AerSimulator()
# Compile the circuit for the simulator
# Transpilation optimizes the circuit for the target backend
compiled_circuit = transpile(qc, simulator)
# Execute the circuit 1024 times
# Multiple runs reveal the probabilistic nature of quantum mechanics
job = simulator.run(compiled_circuit, shots=1024)
# Retrieve and display results
result = job.result()
counts = result.get_counts(compiled_circuit)
print(f"Measurement Results: {counts}")
Interpreting the Results
Sample Output: {'00': 482, '11': 542}
This result demonstrates perfect quantum entanglement:
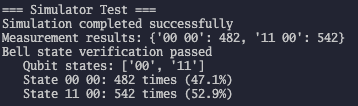
- Only 00 and 11 states observed: No mixed states (01 or 10)
- Close to 50:50 distribution: 47.1 % vs 52.9 % confirms theoretical prediction
- Statistical variation is normal: With 1024 measurements, perfect 50:50 is extremely unlikely
- Correlation proof: When one qubit is 0, the other is always 0; when one is 1, the other is always 1## [Notice Block – Info]
Why Not Exactly 50:50?
Quantum mechanics is fundamentally probabilistic. Even though theory predicts 50% probability for each outcome, any finite number of measurements will show statistical variation. This is normal and expected behavior, not an error in your setup.
With infinite measurements, the ratio would approach exactly 50:50, but with 1024 shots, seeing results like 487:537 or 501:523 is perfectly normal.
Installation Verification
# Complete verification script
import sys
import qiskit
from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator
# Display environment information
print(f"Python version: {sys.version}")
print(f"Qiskit version: {qiskit.__version__}")
# Test basic functionality
try:
# Create and run a simple circuit
qc = QuantumCircuit(1, 1)
qc.h(0)
qc.measure_all()
simulator = AerSimulator()
job = simulator.run(qc, shots=100)
result = job.result()
print("✓ Installation verified successfully")
print("✓ Simulator functioning correctly")
print("✓ Ready for quantum computing!")
except Exception as e:
print(f"✗ Error detected: {e}")
Common Issues and Solutions
Issue: “No module named ‘qiskit_aer'”
Cause: Qiskit 2.0+ separated the Aer simulator into its own package
Solution: Run pip install qiskit-aer
Issue: Permission denied during conda installation
Cause: Incorrect ownership of Anaconda directory Solution:
sudo chown -R $(whoami) /opt/homebrew/anaconda3
chmod -R 755 /opt/homebrew/anaconda3
Issue: Conda command not found
Cause: PATH not properly configured Solution: Add to ~/.zshrc and restart terminal:
export PATH="/opt/homebrew/anaconda3/bin:$PATH"
Issue: Jupyter kernel not showing quantum environmen
Cause: Environment not registered with Jupyter Solution:
python -m ipykernel install --user --name qiskit_env --display-name "Qiskit"
What We Accomplished
- [x] Installed complete quantum computing development environment
- [x] Created isolated Python environment for quantum projects
- [x] Successfully imported and tested all Qiskit components
- [x] Built and executed first quantum circuit
- [x] Observed quantum entanglement in action
- [x] Verified installation with comprehensive testing
“Any sufficiently advanced technology is indistinguishable from magic.” – Arthur C. Clarke
What we’ve just accomplished might seem like magic, but it’s the foundation of quantum computing. You’ve successfully created quantum entanglement and observed one of the most fundamental phenomena in quantum mechanics.
Understanding Your Achievement
The Bell state you created represents something profound in physics. You’ve just demonstrated that:
Two particles can be connected in a way that transcends classical physics. When you measure one qubit and find it in state 0, you instantly know the other is also in state 0, regardless of their physical separation.
This isn’t just a programming exercise – you’ve recreated one of the most important experiments in quantum mechanics history, the foundation for quantum communication, quantum cryptography, and quantum computing itself.